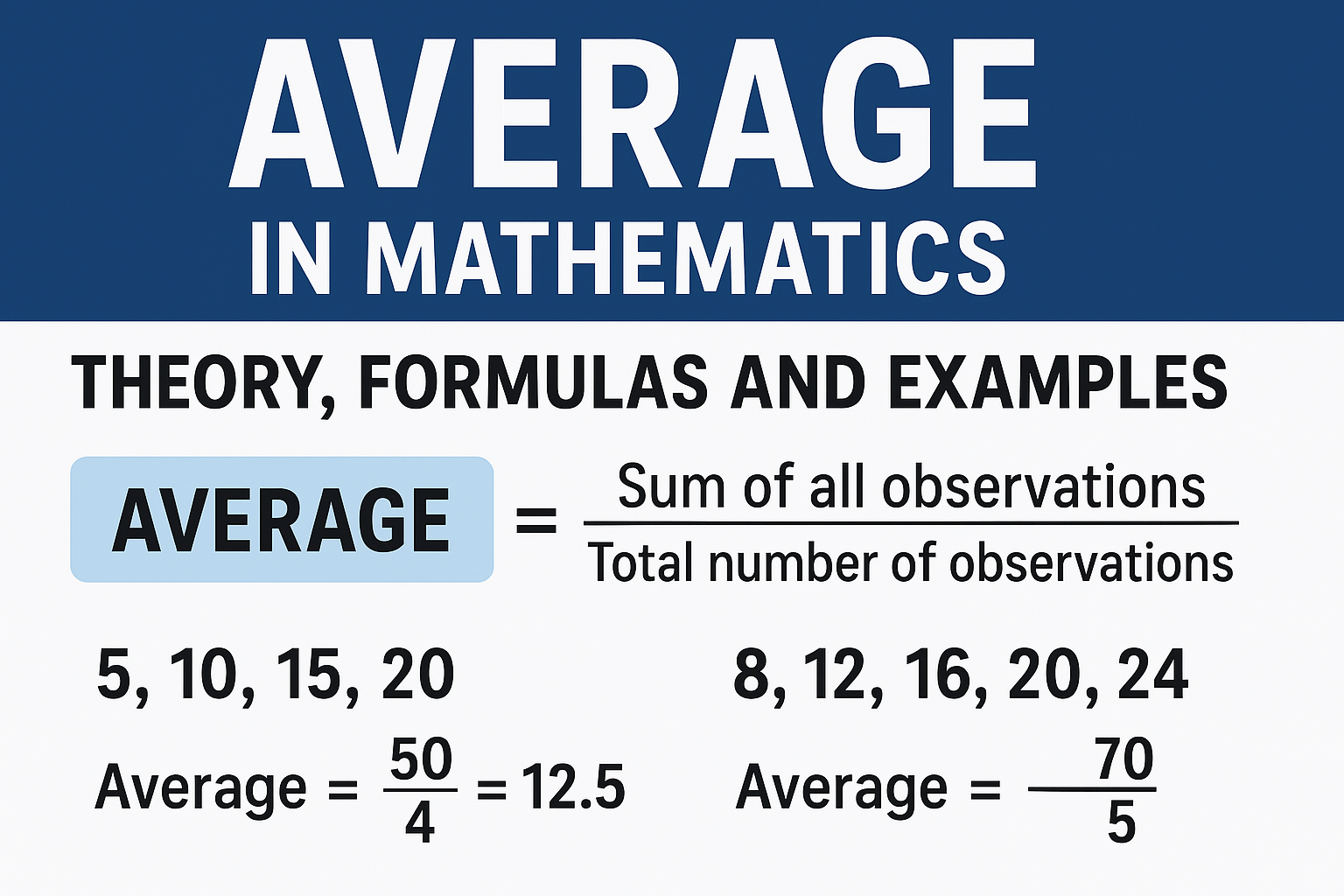DISCLAIMER:-
THIS ARTICLE IS INTENDED SOLELY FOR EDUCATIONAL PURPOSES. ALL EXAMPLES, FORMULAS, AND EXPLANATIONS ARE FOR LEARNING AND PRACTICE. THE WEBSITE OWNER IS NOT RESPONSIBLE FOR ANY EXAM-RELATED DISCREPANCIES, ERRORS, OR CHANGES. USERS SHOULD VERIFY EXAM-SPECIFIC RULES AND QUESTIONS FROM OFFICIAL SOURCES.
1. INTRODUCTION
IN MATHEMATICS, AVERAGE, ALSO CALLED ARITHMETIC MEAN, IS A CENTRAL CONCEPT IN ARITHMETIC AND STATISTICS. IT REPRESENTS THE CENTRAL VALUE OF A SET OF NUMBERS AND HELPS US SUMMARIZE LARGE DATA SETS IN A SINGLE MEANINGFUL NUMBER.
AVERAGE IS NOT JUST A THEORETICAL CONCEPT; IT IS USED IN DAILY LIFE, FINANCE, EDUCATION, SPORTS, RESEARCH AND COMPETITIVE EXAMS LIKE SSC, IBPS, RRB, RAILWAY, UPSC, AND PSU EXAMS.
THIS ARTICLE IS A COMPLETE GUIDE COVERING ALL ASPECTS OF AVERAGES, FROM SIMPLE DEFINITIONS TO COMPLEX EXAM-LEVEL PROBLEMS.
2. DEFINITION OF AVERAGE
MATHEMATICALLY, THE AVERAGE OF A SET OF NUMBERS IS THE SUM OF ALL NUMBERS DIVIDED BY THE TOTAL COUNT OF NUMBERS:
AVERAGE=SUM OF ALL OBSERVATIONS\ TOTAL NUMBER OF OBSERVATION
EXAMPLE 1: SIMPLE AVERAGE
FIND THE AVERAGE OF 5, 10, 15, 20.
SUM = 5 + 10 + 15 + 20 = 50
NUMBER OF TERMS = 4
AVERAGE=50/44=12.5
WHY AVERAGE IS IMPORTANT?
SIMPLIFIES LARGE DATA INTO A SINGLE NUMBER
HELPS IN COMPARING DATASETS
PROVIDES INSIGHT INTO TRENDS AND PERFORMANCE
USED IN EXAMS, FINANCE, RESEARCH AND REAL-LIFE DECISION-MAKING
3. BASIC FORMULA OF AVERAGE
AVERAGE (A)=SUM OF ALL NUMBERS (Σx)/NUMBERS (n)
KEY POINTS:
AVERAGE LIES BETWEEN THE SMALLEST AND LARGEST VALUE OF THE DATASET
AVERAGE CHANGES PROPORTIONALLY IF ALL NUMBERS ARE INCREASED/DECREASED BY A CONSTANT
AVERAGE IS USEFUL TO COMPARE GROUPS OR SUBSETS OF DATA
4. PROPERTIES OF AVERAGES
IF ALL NUMBERS ARE INCREASED BY THE SAME VALUE, THE AVERAGE INCREASES BY THAT VALUE.
IF ALL NUMBERS ARE DECREASED BY THE SAME VALUE, THE AVERAGE DECREASES BY THAT VALUE.
IF ALL NUMBERS ARE MULTIPLIED BY A NUMBER, THE AVERAGE IS MULTIPLIED BY THE SAME NUMBER.
IF ALL NUMBERS ARE DIVIDED BY A NUMBER, THE AVERAGE IS DIVIDED BY THE SAME NUMBER.
AVERAGE ALWAYS LIES BETWEEN THE MINIMUM AND MAXIMUM VALUES OF THE DATASET.
5. TYPES OF AVERAGES
SIMPLE ARITHMETIC AVERAGE
USED FOR EQUALLY WEIGHTED VALUES.
AVERAGE=SUM OF ALL NUMBERS\ COUNT OF NUMBERS
WEIGHTED AVERAGE
USED WHEN NUMBERS HAVE DIFFERENT WEIGHTS (IMPORTANCE).
WEIGHTED AVERAGE=∑wixi/∑wi
Where wi = weight of i-th number, xi = value of i-th number
EXAMPLE:
A STUDENT SCORED 70, 80, 90 IN THREE SUBJECTS, WITH WEIGHTS 2, 3, 5 RESPECTIVELY.
WEIGHTED AVERAGE=(70×2)+(80×3)+(90×5)/2+3+5=(140+240+450)/10=83
MOVING AVERAGE
USED IN TIME SERIES DATA TO ANALYZE TRENDS BY AVERAGING RECENT n OBSERVATIONS.
GROUP AVERAGE
USED WHEN DATA IS GROUPED INTO CLASSES.
AVERAGE=∑fixi/∑fi
Where fi = frequency, xi = class midpoint
6. AVERAGE OF SPECIAL SERIES
FIRST n NATURAL NUMBERS:
AVERAGE=(n+1)/2
FIRST n EVEN NUMBERS:
AVERAGE=n+1
FIRST N ODD NUMBERS:
AVERAGE=n
CONSECUTIVE NUMBERS:
AVERAGE = middle number (for odd count), or mean of middle two (for even count)
7. IMPORTANT FORMULAS FOR EXAMS
| SCENARIO | FORMULA |
| AVERAGE OF n NUMBERS | A=sum of n numbers / n |
| MISSING NUMBER IN SET | x=nA−sum of known |
| NEW AVERAGE AFTER ADDING A NUMBER | Anew=nA+x/n+1 |
| NEW AVERAGE AFTER REMOVING A NUMBER | Anew=nA−x/n−1 |
| WEIGHTED AVERAGE | Aw=∑wixi/∑wi |
| AVERAGE OF CONSECUTIVE NUMBERS | middle number or mean of two middle numbers |
8. SHORTCUT METHODS TO SOLVE AVERAGE PROBLEMS
ASSUMED AVERAGE METHOD
ASSUME ANY NUMBER AS AVERAGE.
CALCULATE DEVIATIONS FROM ASSUMED AVERAGE.
SUM DEVIATIONS AND DIVIDE BY COUNT.
ADD ASSUMED AVERAGE TO GET ACTUAL AVERAGE.
GROUPING METHOD
IF NUMBERS ARE IN GROUPS WITH KNOWN AVERAGES:
Overall average=∑(group average × group size)/total size
USING DIFFERENCES
If numbers differ from a central value, average can be quickly computed using differences from a base number.
9. SOLVED EXAMPLES (STEP-BY-STEP)
EXAMPLE 1
FIND AVERAGE OF 12, 15, 18, 21, 24
SUM = 12+15+18+21+24 = 90
COUNT = 5
AVERAGE = 90/5 = 18
EXAMPLE 2
AVERAGE OF 10 NUMBERS IS 20. FIND TOTAL.
- TOTAL = 10 × 20 = 200
EXAMPLE 3
AVERAGE OF 5 NUMBERS IS 25. ONE NUMBER IS MISSING. THE SUM OF 4 NUMBERS = 80.
TOTAL = 5 × 25 = 125
MISSING NUMBER = 125 – 80 = 45
EXAMPLE 4
A STUDENT SCORES 60, 65, 70, 75 IN FOUR EXAMS. FIND REQUIRED 5TH SCORE FOR AVERAGE 70.
TOTAL NEEDED = 70 × 5 = 350
CURRENT TOTAL = 60+65+70+75 = 270
5TH SCORE = 350-270 = 80
EXAMPLE 5
WEIGHTED AVERAGE: A TEACHER HAS 3 CLASSES WITH 20, 25, 30 STUDENTS. AVERAGE MARKS: 70, 80, 90. FIND OVERALL AVERAGE.
Overall average=(20×70)+(25×80)+(30×90/)20+25+30=1400+2000+2700/75=82
10. ADVANCED PROBLEMS
AVERAGE WITH MISSING DATA
IF SOME VALUES ARE MISSING, USE THE FORMULA:
average=sum of known numbers + sum of missing numbers/n
AVERAGE IN MIXTURES
Two groups with averages a₁ and a₂, counts n₁ and n₂:
New average=n1A1+n2A2/n1+n2
EXAMPLE:
CLASS A: 40 STUDENTS, AVERAGE 50
CLASS B: 60 STUDENTS, AVERAGE 60
OVERALL AVERAGE=40×50+60×60/100=56
CONSECUTIVE NUMBERS
Average = middle number (odd count) or mean of middle two (even count).
EXAMPLE: AVERAGE OF 11,12,13,14,15 = 13
11. APPLICATIONS OF AVERAGE
EDUCATION:-
STUDENT PERFORMANCE, CLASS AVERAGE, EXAM SCORES
FINANCE:-
INTEREST RATES, EMI, STOCK PRICES, BUDGETING
SPORTS:-
BATTING AVERAGE, BOWLING ECONOMY
INDUSTRY:-
PRODUCTION, QUALITY CONTROL
DAILY LIFE:-
EXPENSE TRACKING, RAINFALL, TEMPERATURE, POPULATION
12. PRACTICE QUESTIONS (100+ EXAM LEVEL)
(SAMPLE OF 20 QUESTIONS; FULL 100 CAN BE APPENDED)
- FIND AVERAGE OF 15, 18, 21, 24
- AVERAGE OF 12 NUMBERS = 40, FIND TOTAL
- MISSING NUMBER: AVERAGE OF 7 NUMBERS = 25, SUM OF 6 NUMBERS = 135
- AVERAGE OF 5 EXAMS = 80, LAST EXAM SCORE = ?
- WEIGHTED AVERAGE OF MARKS: 3 SUBJECTS WITH WEIGHT 2,3,5
- AVERAGE OF FIRST 50 NATURAL NUMBERS
- AVERAGE OF FIRST 50 EVEN NUMBERS
- AVERAGE OF FIRST 50 ODD NUMBERS
- CLASS AVERAGE INCREASES BY 2 WHEN NEW STUDENT JOINS, FIND STUDENT MARKS
- SUM OF 10 NUMBERS = 400, FIND AVERAGE
- AVERAGE OF CONSECUTIVE NUMBERS 20 TO 30
- AVERAGE RAINFALL OF WEEK: 7,8,12,9,10,6,15
- AVERAGE OF 4 CONSECUTIVE NUMBERS = 25, FIND NUMBERS
- WEIGHTED AVERAGE IN INVESTMENTS: 3 INVESTMENTS, 50K, 70K, 30K WITH DIFFERENT RETURNS
- AVERAGE MARKS OF 50 STUDENTS = 45, 5 HIGHEST SCORERS REMOVED, NEW AVERAGE = ?
- AVERAGE HEIGHT OF 10 PERSONS = 170 CM, ONE TALLER 190 CM LEAVES, NEW AVERAGE = ?
- WEIGHTED AVERAGE: PRODUCE 2 FACTORIES, 1000 UNITS 50%, 2000 UNITS 60% EFFICIENCY
- AVERAGE AGE OF 6 PERSONS = 25, 1 LEAVES 35, FIND NEW AVERAGE
- AVERAGE SPEED OF TWO TRIPS 50 KM/H AND 70 KM/H
- AVERAGE COST PRICE OF 5 ITEMS = 200, DISCOUNT APPLIED, NEW AVERAGE = ?
13. TIPS & TRICKS FOR EXAMS
ALWAYS CHECK FOR TOTAL SUM FIRST
USE ASSUMED AVERAGE FOR LARGE NUMBERS
GROUP NUMBERS TO SAVE CALCULATION TIME
REMEMBER PROPERTIES OF AVERAGE TO SIMPLIFY QUESTIONS
WEIGHTED AVERAGE PROBLEMS OFTEN APPEAR IN PSU & BANKING EXAMS
14. SUMMARY & CONCLUSION
AVERAGE IS A FUNDAMENTAL MATHEMATICAL CONCEPT USED TO SUMMARIZE DATA. FROM SCHOOL-LEVEL ARITHMETIC TO COMPETITIVE EXAMS AND REAL-LIFE APPLICATIONS, MASTERING AVERAGES PROVIDES ACCURACY, SPEED, AND INSIGHT INTO DATA.
THIS ARTICLE COVERS:
DEFINITION & IMPORTANCE
FORMULAS & PROPERTIES
SIMPLE, WEIGHTED, MOVING AVERAGES
SPECIAL SERIES AVERAGES
ADVANCED AND EXAM-LEVEL PROBLEMS
REAL-LIFE APPLICATIONS
CLICK TO APPLY:
Click the application link below:
👉 Apply Here for SBI Credit Card (Referral Code: 243zfQ0yYm3)